Zadania projektowe do przedmiotu POR (na semestr zimowy 2006 roku)

prowadzący: Ewa Niewiadomska-Szynkiewicz (e-mail: e-n-s@ia.pw.edu.pl, pokój 572),

konsultacje: czwartki godzina 10.00 – 12.00

(nazwisko) oznacza, że zadanie jest już wybrane

Aplikacje mogą być realizowane z wykorzystaniem następujących mechanizmów:

· pamięć dzielona: wątki POSIX, wątki w języku Java, OpenMP dla programów w języku C

· pamięć rozproszona: MPI, RPC (jeżeli pierwsza część była realizowana w wątkach w języku Java, druga nie może być wykonana z wykorzystaniem RMI)

Osoby zainteresowane realizacją wymienionych zadań projektowych są proszone o zgłoszenie się po materiały pomocnicze.

Uwaga! Nominalny czas zakończenia i oddania projektu do końca semestru (ostatni dzień przed rozpoczęciem sesji).

W przypadku opóźnienia oddania projektu ocena jest obniżona o 1.

Metody optymalizacji wypukłej. Zadania dotyczą równoległej implementacji różnych metod poszukiwania lokalnego minimum (maksimum) w Rⁿ. Należy zaproponować dwa różne sposoby zrównoleglenia algorytmów (wersja synchroniczna i asynchroniczna) i wykonać testy dla podanych funkcji.

Zadania:

1 Metoda sympleksu nieliniowego w wersji równoległej (algorytm opracowany przez p. V. Torczon). Ocenić przyspieszenie obliczeń w zależności od stopnia zrównoleglenia (sprawdzić – dla większych wymiarów – wpływ liczności wierzchołków, przydzielanych do jednego procesora na szybkość obliczeń). Wykonać testy dla funkcji A i B (dla n=5, 10, 20, 50, 100).(G. Pusz, Ł. Szejba)

A Funkcja testowa 4-tego stopnia

B Funkcja Rosenbrocka

2 Metoda optymalizacji z ograniczeniami Complex-Box (metoda wykorzystująca przekształcanie wielościanu utworzonego przez punkty wybierane z obszaru poszukiwań). Metoda sprawdza spełnienie ograniczeń. Rozwiązać zamieszczone poniżej zadania: Zad. 1 i Zad. 2. (dla n=5, 10, 20, 50, 100).(A. Gerula, ...)

Zad. 1

Zad. 2

Metody optymalizacji niewypukłej. Zadania dotyczą równoległej i rozproszonej implementacji różnych metod poszukiwania globalnego minimum (maksimum) w Rⁿ. Należy zaproponować dwa różne sposoby zrównoleglenia algorytmów (wersja synchroniczna i asynchroniczna) i wykonać testy dla podanych funkcji.

Zadania:

3 Metoda optymalizacji wielostartowej polegająca na równoległym losowaniu poszukiwań i wyznaczaniu najlepszych punktów (min/max) w tych kierunkach. Wynik – najlepszy (w sensie zadanego kryterium) wyznaczony punkt. Do wyznaczenia minimum w kierunku zastosować metodę interpolacji kwadratowej lub złotego podziału. Wykonać testy dla funkcji C i D (dla n=2, 10, 20, 50, 100). (J. Lipowski, M. Grzębski)

4 Hybrydowa metoda losowa – połączenie metody sterowanego przeszukiwania losowego i metody symulowanego wyżarzania SA. Wykonywane są kolejno operacje losowania i przekształcania kompleksu utworzonego z punktów wylosowanych z obszaru poszukiwań oraz w przypadku znalezienia lepszego rozwiązania, uruchamiany jest algorytm SA. (równolegle). Wykonać testy dla funkcji C i D (dla n=2, 10, 20, 50, 100). (T. Kaczyński, M. Kurcz)

5 Optymalizacja sieci za pomocą algorytmu ewolucyjnego. (K. Ostolski)

6 Algorytm koewolucyjny (wersja algorytmu genetycznego z kodowaniem binarnym lub strategii ewolucyjnej z kodowaniem rzeczywistoliczbowym – do wyboru). Operujemy na kilku populacjach punktów. Populacje co pewien okres czasu wymieniają między sobą informacje. Wykonać testy dla funkcji D i E (dla n=2, 10, 20, 50, 100). (W. Wasiak, P. Malinowski)

C Funkcja Rosenbrocka

D. Funkcja Griewanka

·

. Ma minimum globalne , w punkcie .

E. Funkcja Acleya

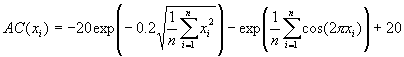
. Ma minimum globalne , w punkcie .

Zastosowania.

Zadania:

7 Rozwiązanie zadania komiwojażera za pomocą algorytmu genetycznego. (P. Simiński, M. Wyrzyk)

8 Zaproponować optymalny dla firmy (maksymalizujący zysk ze sprzedaży) rozdział środków na reklamę jej produktów w radiu, telewizji i prasie. Wykorzystać nieliniowy model sprzedaży. Do rozwiązania zadania optymalizacji zastosować metodę poszukiwań losowych CRS2. (M. Rosiewicz i P. Mochocki)

Symulacja rozproszona.

Zadania:

9 Algorytm symulacji rozproszonej asynchronicznej MTW (Moving Time Windows) – metoda z zawijaniem czasu na oknach. (Ł. Bamburski, K. Żukowski)

Identyfikacja.

Zadania:

10 Algorytm identyfikacji bazujący na metodzie PCA. (J. Florczuk)